La scène étalée sous l'oeil de notre système a maintenant été visualisée, analysée et interprétée. Toutes les informations pertinentes concernant le monde manipulable est disponible. A présent il faut décider que faire de tous ces objets.
Nous allons adapter le principe de la carotte et du bâton à l'ordinateur. Pour ce faire, on observe à chaque cycle l'évolution de la situation. En fonction de celle-ci nous attribuerons ou non une récompense. Le but du programme d'apprentissage est alors de maximiser les récompenses obtenues, c'est à dire d'adopter un comportement, de réaliser les actions qui apportent une récompense, soit, les actions qui rapprochent du but.
A partir de la description de l'environnement, on commence par déterminer la
situation où l'on se trouve. Connaissant toues les actions possibles pour cette
situation, on choisit la plus prometteuse.
Comment
déterminer l'action la plus prometteuse ? A chaque couplet situation-action
possible (que nous nommerons maintenant règle, qui peut s'exprimer par : SI
Situation = A Alors Action = 8), on attribut une force. Cette force sera le
produit de l'historique des récompenses reçues lorsque la règle en question est
utilisée. Elle est altérée par la valeur de la récompense reçue :
- soit RS,A(t) la force de la règle Si S Alors A à instant t. Supposons que cette règle soit choisie à l'instant t+1, et soit R la valeur de la récompense obtenue.
- Alors RS,A(t+1) = aRS,A(t)+(1-a)R, a E [0;1].
S'il y a récompense (R non nul) la force augmente, sinon elle
diminue. On attribut également un poids à toute règle. La somme des poids est
constante et également répartie sur toutes les règles au départ.
Ces poids vont traduire
l'utilisation des règles indépendamment de leur force. Quand une règle est
utilisée on augmente sont poids (tout en diminuant le poids d'une autre règle,
la moins forte, pour conserver la somme des poids constante). Ainsi plus une
règle est forte, plus elle aura de chances d'être utilisée, et donc plus son
poids risque d'augmenter. La connaissance du poids et de la force de chaque
règle va permettre, à chaque itération de choisir
une action.
Une interprétation possible de ce fonctionnement est l'algorithme génétique [Hol 75]. L'individu a pour code génétique une règle et pour force, celle de la règle telle qu'elle vient d'être présentée. Le poids devient l'effectif de l'individu dans la population de taille fixe (la taille de la population est donc égale à la somme des poids). Lors de l'utilisation d'une règle, on duplique alors l'individu correspondant dans la population et on élimine un représentant de la plus mauvaise règle. Dans ce cas de figure, c'est l'opérateur de sélection de l'algorithme génétique qui choisi l'action à effectuer.
Pour de grands nombres de situations et d'actions possibles, le nombre de règles devient vite très important. Il est alors possible de généraliser les règles afin de réduire leur nombre. Si pour deux situations A et B, l'action 5 est très efficace, il peut être judicieux de remplacer les règles Si A alors 5, et Si B alors 5, par Si A ou B alors 5.
De plus, si l'apprentissage est fondé sur un algorithme génétique il n'est pas nécessaire d'avoir un représentant de chaque règle possible. Les capacités d'exploration propres à ce type d'algorithme par le biais du croisement et de la mutation permet de générer constamment de nouvelles règles. Si cela fonctionne très bien sur des problèmes simulés, mais pour un problème concret comme le nôtre il faudrait pouvoir évaluer très rapidement les règles, c'est à dire sans réaliser toutes les actions qu'elles impliquent.
Comme le nombre de règle dans notre cas n'est pas trop important et ces procédés d'induction [Col 96] ne seront plus abordés.
Connaissant la situation S du système, il nous faut maintenant choisir la bonne action. Cette décision peut se faire selon l'une des trois stratégies suivantes à l'aide de la force des règles possibles (celles dont S est la condition) et éventuellement à l'aide de leur poids.
- On note :
- P(i) = Probabilité de choisir l'action i,
- RS,i = force de l'action i pour la situation S,
- PS,i = poids de l'action i pour la situation S.
- Stratégie 1 :
- Soit
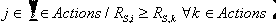
- P(j) = 0.9 et P(i) =
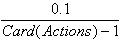
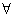 i,j
i,j
- Soit
- Stratégie 2 :
- Pour chaque action j : P(j) =
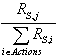
- Pour chaque action j : P(j) =
- Stratégie 3 :
- Pour chaque action j : P(j) =
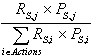
- Pour chaque action j : P(j) =
Selon le fonctionnement décrit dans le premier paragraphe de ce chapitre, une récompense est attribuée à chaque itération et le force de la dernière règle utilisée n'est fonction que de cette rétribution. La force peut être vue comme une probabilité de recevoir une bonne récompense se basant sur les expériences antérieures (attention ce n'est qu'une interprétation et non une vérité mathématique). Quand l'ordinateur utilise une règle de force 0.72, il espère à 72 % (nos récompenses sont toujours comprises entre 0 et 1 inclus, les forces le sont donc également) que l'action sera un succès, i.e. qu'elle va générer une récompense.
Pourtant, il est parfois préférable de choisir une action moins gratifiante, mais qui permet d'atteindre une situation plus avantageuse (en présence d'obstacles notamment). Nous n'allons donc plus donner une récompense à chaque itération mais la retarder toutes les n actions effectuées. Quand aucune récompense n'est attribuée, la force de la dernière règle choisie est ajournée en fonction de la prochaine règle choisie. Le système va alors apprendre des enchaînements d'action au lieu d'agir coup par coup.
Le Q-learning [ref ??] propose lui d'ajourner la dernière règle choisie avec la force de la meilleure règle conditionnée par la situation atteinte. La force attribuée n'a par conséquent plus du tout la même signification et traduirait plutôt une probabilité d'atteindre une situation plus avantageuse.
Il est important de comprendre que la force n'exprime pas la même chose d'une méthode à l'autre (cf. exemples au paragraphe 3.6.2). Cette différence explique les comportements spécifiques observés pour chacune de celles-ci.
Voici maintenant l'algorithme dit du bandit manchot, étendu au principe des récompenses retardées.
- Observer la situation : S
- Choisir l'action initiale : A (au hasard)
- Tant que
le but n'est pas atteint faire :
- Effectuer l'action A (transmettre l'ordre d'agir au robot)
- Dupliquer l'action effectuée, i.e. si possible augmenter son poids de 1 et diminuer celui de la moins forte action pour cette situation.
- Observer la nouvelle situation : S' (dans notre cas, déterminer S' en fonction de la liste d'objets fournie par la perception)
- Choisir la prochaine action : A'
- Toutes
les n actions faire :
- Si
Amélioration de la situation
Alors
- R := 1
- R := 0
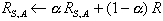
- Si
Q-learning Alors
- A'' := A
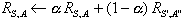
- Si
Amélioration de la situation
Alors
- A := A'
- S := S'
La manière dont les forces évoluent et donc l'efficacité de l'algorithme dépendent fortement du paramètre alpha :
- Si alpha = 1, les forces n'évoluent plus et la machine n'apprend rien.
- Si alpha = 0, les forces sont égales à la récompense reçue lors de la dernière utilisation de la règle correspondante. L'algorithme ne tient plus compte de son histoire.
Pour la suite nous avons fixé alpha = 0.8
Que se passe-t-il, lorsqu'on utilise la troisième stratégie de décision (cf. paragraphe 3.2), si une règle très efficace tout au long d'un long apprentissage devient tout à coup complètement inefficace ?
Jusqu'à ce changement des propriétés de l'environnement (la réponse aux actions n'est plus celle attendue), la règle en question bénéficiait d'un poids maximal et d'une force très élevée. Pour que le système soit de nouveau capable, il doit réapprendre : réajuster force et poids. Il faudra beaucoup de temps pour que la force baisse suffisamment pour rendre cette action défaillante moins probable que les autres. Il peut alors se révéler judicieux de détecter ce problème plus tôt. Pour cela, quand une action échoue, on examine force et poids pour voir s'ils sont en contradiction. Une règle faible ne doit pas être utilisée, son poids doit donc être également faible. Si on observe alors un poids fort, pour une force peu élevée, on redistribue le poids sur les autres règles ayant la même condition, i.e. celles correspondant à la même situation.
Pour mettre au point ces algorithmes et décider des paramètres, nous avons bâti une simulation qui sera le support du système final (il suffira d'adapter l'observation et l'action). Cette simulation est disponible sur la disquette jointe (\learn\apprent.exe).
L'ordinateur doit apprendre à déplacer un objet, symbolisé à l'écran par un O, vers une cible symbolisée par un X, jusqu'à ce qu'ils coïncident. Pour cela il dispose de neuf actions élémentaires : se déplacer de la valeur d'un caractère vers le haut, le bas, la droite, la gauche, en diagonale, ou bien ne rien faire. Et, il perçoit neuf situations, selon les positions relatives de l'objet et de la cible : cible atteinte, cible plus haut, cible plus basse...
La récompense attribuée est 1 si la distance de l'objet à la cible diminue, 0 sinon.
La cible est soit fixe, soit mouvante (mouvement cyclique décrit par des équations paramétriques), soit déplacée aléatoirement si certaines actions sont choisies.
Le simulateur a permis d'expérimenter chacune des méthodes d'apprentissage que nous avons décrites. Toutes ont été capables d'apprendre à résoudre chaque problème posé, et de s'adapter de l'un à l'autre (changement de problème sans ré initialiser la base d'apprentissage, on simule ainsi une évolution des caractéristiques de l'environnement). Cependant , les stratégies 1 et 2 n'ont pas beaucoup été utilisées car, même si elles peuvent se révéler aussi efficace que la dernière, celle-ci, prenant en compte les poids des règles, permet un apprentissage plus nuancé. En effet la force d'une règle ayant été utilisée une ou deux fois est moins signifiante que la force d'une règle utilisée à de nombreuses reprises.
L'heuristique présentée au paragraphe 3.5 a parfaitement rempli sa tâche lors d'un apprentissage par renforcement simple avec variations de l'environnement (changements de problème). L'apprentissage n'est pas ralenti et la prise en compte d'une variation d'efficacité d'une règle est plus rapide. Son efficacité ne s'est toutefois pas révélée appréciable dans le cas d'un apprentissage par renforcement retardé. Les qualités de celui-ci n'ont cependant pas été altérées.
Pour comparer plus en détail ces différents apprentissages il serait intéressant de leur soumettre des problèmes plus subtils où l'efficacité des solutions adoptées dépendrait par exemple, du nombre d'actions effectuées en tenant compte d'un coût associé à chacune d'entre celles-ci...
Pour notre application un apprentissage par renforcement simple devrait remplir parfaitement son rôle: il est relativement rapide et le comportement appris, s'il manque parfois de subtilité (foncer droit sur la cible) est cependant dans la majorité des cas le plus efficace.
Pour illustrer les quelques différences des trois méthodes (renforcement simple, renforcement retardé et q-learning), elles ont été soumises au même problème : atteindre cent fois une cible fixe en utilisant la troisième stratégie de décision (pour laquelle les poids influent sur le choix des actions). C'est un problème facile dans le sens où aucune perturbation n'interfère avec les actions menées et l'effet de chacune de celles-ci est parfaitement déterministe et constant.
Remarque : l'état de la base d'apprentissage montré dans les tableaux illustrant les trois exemples indique les valeurs de force et de poids de chaque règle à la fin des itérations. Ce n'est pas un état stable et il reprendrait ses évolutions si on soumettait le système à une nouvelle série d'itérations.
Comment lire les tableaux suivants :
| ... | Action | ... | |
| ... | ... | ... | ... |
| Situation | ... | Force Poids |
... |
| ... | ... | ... | ... |
Ces tableaux montrent l'état de la base d'apprentissage après 100 itérations. Une itération étant une atteinte de cible. Le nombre d'actions effectué diffère à chaque action et tend à diminuer au cours de l'apprentissage. Les couples situation-action ayant une force importante (supérieure à 0.90) sont indiqués en gras. L'italique indique que l'action correspondante est la plus utilisée dernièrement pour la situation indiquée sur la même ligne, c'est à dire l'action de poids le plus fort pour la situation donnée.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
| 1 | 0.16 1 |
0.94 1 |
0.26 1 |
0.20 1 |
0.65 1 |
0.20 1 |
0.20 1 |
1.00 82 |
0.16 1 |
| 2 | 0.32 1 |
0.38 1 |
0.16 1 |
0.16 1 |
1.00 82 |
0.36 1 |
0.87 1 |
1.00 1 |
0.40 1 |
| 3 | 0.20 1 |
0.26 1 |
0.20 1 |
0.10 1 |
0.80 1 |
0.99 1 |
1.00 82 |
0.20 1 |
0.16 1 |
| 4 | 0.16 1 |
0.40 1 |
0.32 1 |
0.16 1 |
0.26 1 |
1.00 82 |
1.00 1 |
0.16 1 |
0.99 1 |
| 5 | 0.26 6 |
0.26 1 |
0.60 14 |
0.32 12 |
0.26 11 |
0.77 19 |
0.40 11 |
0.20 1 |
0.84 15 |
| 6 | 0.32 1 |
0.93 1 |
0.97 1 |
1.00 1 |
0.16 1 |
0.26 1 |
0.20 1 |
0.13 1 |
1.00 82 |
| 7 | 0.32 1 |
0.93 1 |
1.00 1 |
1.00 82 |
0.16 1 |
0.20 1 |
0.20 1 |
0.26 1 |
0.20 1 |
| 8 | 0.26 1 |
1.00 1 |
0.66 1 |
1.00 82 |
0.13 1 |
0.10 1 |
0.13 1 |
1.00 1 |
0.10 1 |
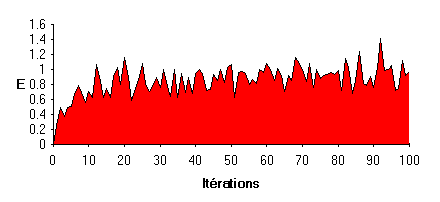 |
Efficacité : E=D/A D : Distance initiale A : nombre d'actions pour atteindre la cible |
Comportement adopté :
- L'objet
atteint la cible par déplacements verticaux et horizontaux : il se place sur la
même ligne, ou colonne puis fonce droit sur celle-ci.
Les déplacements en diagonal sont très rarement adoptés. - L'apprentissage est très rapide.
On observe un comportement efficace dès la dixième itération.
Les forces sont directement en relation avec l'efficacité des règles.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
| 1 | 0.64 1 |
0.70 1 |
0.66 1 |
0.66 1 |
0.73 1 |
0.76 1 |
0.69 1 |
0.71 82 |
0.54 1 |
| 2 | 0.68 1 |
0.67 1 |
0.74 1 |
0.72 1 |
0.71 1 |
0.58 1 |
0.72 82 |
0.73 1 |
0.70 1 |
| 3 | 0.50 1 |
0.59 9 |
0.45 1 |
0.53 1 |
0.70 27 |
0.71 16 |
0.57 1 |
0.39 1 |
0.78 33 |
| 4 | 0.64 1 |
0.43 1 |
0.68 1 |
0.76 1 |
0.87 82 |
0.58 1 |
0.59 1 |
0.79 1 |
0.42 1 |
| 5 | 0.58 1 |
0.63 1 |
0.62 1 |
0.69 1 |
0.52 1 |
0.79 82 |
0.68 1 |
0.69 1 |
0.65 1 |
| 6 | 0.67 1 |
0.47 1 |
0.63 1 |
0.80 82 |
0.76 1 |
0.33 1 |
0.56 1 |
0.69 1 |
0.52 1 |
| 7 | 0.35 1 |
0.45 1 |
0.45 1 |
0.31 1 |
0.42 1 |
0.43 1 |
0.29 1 |
0.48 1 |
0.75 82 |
| 8 | 0.69 1 |
0.75 1 |
0.58 82 |
0.71 1 |
0.80 1 |
0.58 1 |
0.64 1 |
0.75 1 |
0.59 1 |
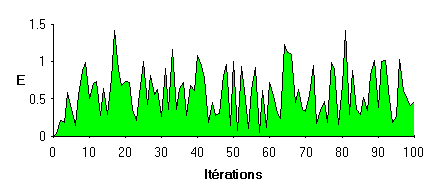 |
Efficacité : E=D/A D : Distance initiale A : nombre d'actions pour atteindre la cible |
Comportement adopté :
- Beaucoup plus nuancé que pour l'exemple 1, il utilise toutes les actions possibles pour atteindre la cible. Les trajectoires sont en général moins directes. On observe des "tâtonnements" avant de foncer droit sur la cible. L'efficacité est donc très variable.
- L'apprentissage est légèrement
plus long que pour l'exemple précédent et n'est pas acquis. La machine est
alors capable du meilleur comme du pire.
Les forces sont ici beaucoup plus nuancées. Ni très élevés ni très faibles, elles ne traduisent pas directement l'efficacité réelle d'une action.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
0.50 10 |
| 1 | 0.95 1 |
0.77 1 |
0.96 1 |
0.77 1 |
0.97 82 |
0.95 1 |
0.89 1 |
0.51 1 |
0.93 1 |
| 2 | 0.94 1 |
0.97 1 |
0.94 1 |
0.93 1 |
0.98 1 |
0.99 1 |
0.91 1 |
0.92 1 |
0.92 1 |
| 3 | 0.95 1 |
0.93 1 |
0.89 1 |
0.95 1 |
0.92 1 |
0.98 82 |
0.98 1 |
0.88 1 |
0.99 2 |
| 4 | 0.63 1 |
0.60 1 |
0.79 1 |
0.62 1 |
0.74 1 |
0.82 1 |
0.91 1 |
0.65 1 |
0.94 82 |
| 5 | 0.78 1 |
0.86 28 |
0.76 1 |
0.55 1 |
0.84 34 |
0.58 1 |
0.90 22 |
0.67 1 |
0.76 1 |
| 6 | 0.64 1 |
0.93 1 |
0.91 82 |
0.83 1 |
0.77 1 |
0.83 1 |
0.74 1 |
0.46 1 |
0.59 1 |
| 7 | 0.94 1 |
0.91 1 |
0.84 82 |
0.68 1 |
0.93 1 |
0.90 1 |
0.73 1 |
0.82 1 |
0.97 1 |
| 8 | 0.99 1 |
0.94 1 |
0.97 1 |
0.99 3 |
0.99 1 |
0.99 2 |
0.97 1 |
0.98 78 |
0.99 2 |
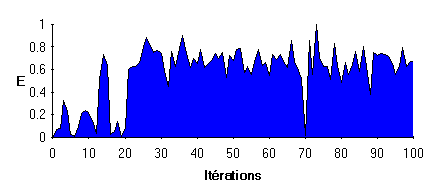 |
Efficacité : E=D/A D : Distance initiale A : nombre d'actions pour atteindre la cible |
Comportement adopté :
- Très régulier ; l'objet tourne autour de la cible, en général dans le même sens, jusqu'à atteindre une situation (toujours la même) où il fonce droit sur la cible.
- L'apprentissage est très long
(>20 itérations) mais est très stable par la suite.
La notion de force est ici totalement différente. Toutes les actions peuvent être fortes (cf. situation 8) car chacune d'entre elles permet d'atteindre une situation où il existe une règle efficace.