La première étape du système est de rechercher, d'extraire de l'environnement l'information nécessaire et utile à la prise de décision. Dans notre cas il s'agira de percevoir les objets qui composent la scène, quels sont-ils et où se trouvent-ils. Le système n'a aucune connaissance au départ et devra acquérir la capacité de reconnaître les formes des objets qui lui sont présentés. Il devra donc se constituer un catalogue, que nous nommerons dictionnaire, des différentes formes rencontrées au fur et à mesure du processus.
L'interprétation de l'image perçue via la caméra vidéo ne pourra commencer qu'après avoir transformé cette image afin qu'elle devienne facilement exploitable, c'est-à-dire pouvoir aisément isoler les objets composant la scène du reste (fond ou bruit) :
- Soit un pixel p, correspond-il à un objet ?
- Si oui, quels sont les autres pixels qui composent l'image de cet objet ?
Une fois les images de chaque objet isolées, on leur fera subir des transformations géométriques afin de rendre le processus de reconnaissance insensible aux facteurs d'échelle, d'orientation et de localisation.
Enfin, l'apprentissage des formes pourra avoir lieu ainsi que la récolte des informations pertinentes pour la suite.
Le traitement comporte donc quatre phases :
- traitement de l'image brute pour réduire les incidences du bruit et la préparer à la recherche des formes
- extraire les différentes formes correspondant aux objets qui constituent la scène à visualiser
- normalisation des formes pour pouvoir identifier une même forme malgré une position et/ou une orientation différente (on en profitera pour déterminer la position et l'orientation des objets)
- classification des formes normalisées et constitution d'un dictionnaire de prototypes.
Diagramme du système de reconnaissance des formes
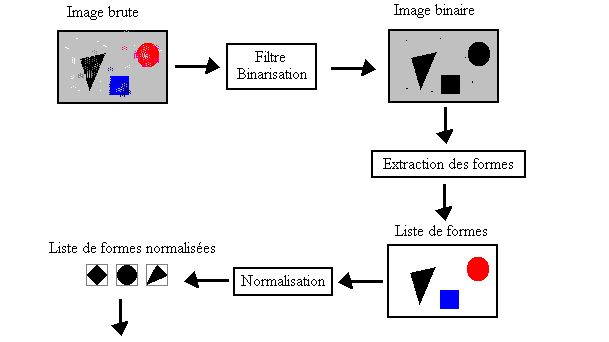
L'image fournie par la caméra vidéo n'est pas directement utilisable après numérisation. Le tableau à deux dimensions de pixels obtenu devra subir éventuellement un pré traitement de type filtrage par moyenne afin d'éliminer du bruit. Cependant si la prise de vue est de bonne qualité, il sera possible d'éviter cette étape.
Ensuite, pour extraire les formes correspondant aux objets, il faut distinguer dans un premier temps les pixels appartenant à un objet des pixels du fond de l'image. Celle-ci sera donc binarisée (un pixel ne pourra avoir qu'une de ces deux valeurs : FOND ou FORME). Pour effectuer ce traitement il faut d'abord connaître les caractéristiques en termes de niveau de gris de l'arrière-plan. On supposera que l'aire de prise des objets sera bien cadrée par la caméra, c'est-à-dire qu'aucun objet ne devra être présent en bordure de l'image. Cela suppose aussi que le fond soit suffisamment homogène et uniforme, c'est à dire qu'il présente le même niveau de gris moyen (au moins) au centre de l'image et en bordure de l'image.
| Exemples de cadrage | |
 | |
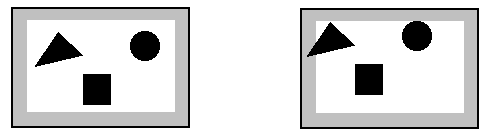| Bon cadrage | Mauvais cadrage |
Aucun objet ne
doit se trouver dans le cadre (zone grisée) utilisé pour déterminer les
caractéristiques du fond. Le triangle dans la deuxième image va perturber
l'analyse statistique et les valeurs du niveau de gris moyen et de l'écart-type
du fond s'en trouvent altérés.
statistique du niveau de gris des pixels constituant cette bordure pour obtenir
le niveau de gris moyen du fond ainsi que l'écart-type associé. La binarisation
découle de cette étude. Elle affecte à chaque pixel la valeur FOND si le niveau
de gris du pixel est dans l'intervalle [NdG moyen - écart-type ; NdG moyen +
écart-type] et la valeur FORME sinon.
Mais, si l'image est trop
bruitée, l'application du filtre de type moyenne qui aura pour effet de
recentrer la valeur des pixels du fond vers le niveau de gris moyen de celui-ci
redevient nécessaire avant la binarisation pour éliminer des points parasites
qui pourrait être pris pour une forme lors des étapes suivantes.
Cependant les bruits parasites ne sont pas la seule cause possible à une hétérogénéité du fond. Ceci peut se produire malgré une très bonne prise de vue, selon la texture de l'aire de travail et de son éclairage.
L'image binaire obtenue à l'étape précédante va être balayée à la recherche des zones connexes de l'image. En effet à chaque zone connexe correspond une forme qui est l'image d'un objet à manipuler (sauf si deux objets sont empilés ou accolés, dans ce cas l'algorithme ne verra qu'un objet là où il y en a plusieurs). Une forme est déterminée par la liste des pixels qui la composent. Dès la détection d'un point ayant la valeur FOND comme niveau de gris, on utilisera un algorithme analogue aux méthodes de remplissage des logiciels de dessin pour extraire tous les pixels appartenant à la même forme connexe que lui.
L'algorithme suivant se charge de construire à partir de l'image binaire une liste de forme, chaque forme étant elle-même une liste de pixels.
- Soient :
- Lformes la liste des formes extraites.
- Lcandidats la liste des pixels candidats pour appartenir à la forme en cours d'extraction.
- Lacceptés la liste des pixels acceptés comme appartenant à la forme en cours d'extraction.
- Initialisation des listes :
Lformes := vide, Lcandidats := vide, Lacceptés := vide. - Pour tout pixel p de l'image binaire faire :
- Si p != FOND et p != VU Alors :
- Lcandidats := Lcandidats + p.
- p := VU
- Tant queLcandidats n'est pas vide faire :
- extraire pixel p' de Lcandidats.
- Lacceptés := Lacceptés + p'.
- Pour tout voisin p'' de p' faire :
- Si p'' != FOND et p'' != VU alors :
- Lcandidats := Lcandidats + p''.
- p'' := VU.
- Si p'' != FOND et p'' != VU alors :
- Lformes := Lformes + Lacceptés (*)
- Lacceptés := vide
- Si p != FOND et p != VU Alors :
- Fin
(*) On insère la forme extraite dans la liste seulement si la liste des pixels acceptés contient plus d'une dizaine d'élément. Il peut en effet subsister des taches parasites après filtrage et binarisation.
Chaque forme extraite à l'étape précédente va maintenant subir une normalisation afin de pouvoir être comparée aux prototypes de formes appris. Cette normalisation comprend trois étapes :
- translation : on déplace la forme pour faire coïncider son centre de gravité avec l'origine.
- rotation.
- homothétie : réduction de la forme (ou agrandissement) à la taille de la matrice prototype.
Ce traitement permettra de comparer des objets malgré des orientations ou des tailles différentes.
Pour chaque forme :
- recherche du centre de gravité :
avec n : nombre de pixels de la forme. - translation de la forme par le vecteur v=(-Gx,-Gy)
- recherche de l'orientation de la forme :
- P := pixel le plus éloigné de G
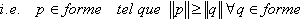
- angle := arctan(|Py|/|Px|)
- P := pixel le plus éloigné de G
- rotation de la forme de -angle. Pour tout pixel p de la forme :
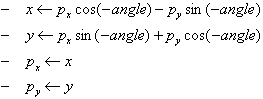
- Calcul du facteur de normalisation (facteur de l'homothétie que doit subir la
forme) :
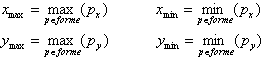
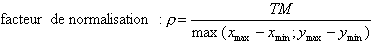
où TM est la dimension d'une matrice prototype. - Si le facteur de normalisation est inferieur à 1 alors réduction sinon agrandissement
- homothétie : construction de la matrice TM x TM qui constitue la forme normalisée à partir de la liste des pixels de la forme originelle.
- Enfin, retourner la position de la forme, sa taille, son orientation ainsi que la matrice contenant sa version normalisée qui devra être comparée avec les prototypes.
ART 1 (Adaptive Resonance Theory) est une architecture développée par G. Carpenter et S. Grossberg [C&G 83]. Cet algorithme d'apprentissage acquière ses connaissances à partir d'exemples, et repose sur deux définitions de distance, c'est à dire de ressemblance, entre les vecteurs examinés (étapes 3 et 3'). Ceci afin d'assurer une stabilité des prototypes du dictionnaire : le but est d'éviter leur évolution cyclique en ne leur permettant d'évoluer que dans un seul sens. Enfin, l'algorithme tel qu'il est décrit ci-après ne s'applique qu'à des vecteurs binaires ; particulièrement au niveau de la mise à jour d'un prototype (étape 4).
- Etape 0 : initialiser le dictionnaire D vide.
- Etape 1 : soit I le prochain vecteur d'entrée, et D' l'ensemble des prototypes candidats égal à D.
- Etape 2 :
trouver le prototype le plus proche de I, c'est-à-dire, trouver
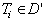qui maximise 
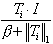avec
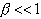. - Etape 3 :
si D'={}, ou si Ti est trop éloigné de I :
,
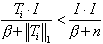où n est la dimension des vecteurs, alors créer un nouveau
prototype Tj. D D {Tj}. Editer j,
puis aller à l'étape 1. - Etape 3'
: si Ti ne correspond pas à I, i.e.
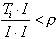, où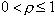 
, alors D'
D'-{Ti} et aller à
l'étape 2. - Etape 4 : sinon (Ti est suffisamment proche de I selon les deux définitions), mettre à jour Ti ; Ti Ti I. Editer i, aller à l'étape 1
Les valeurs de ? et ? définissent les seuils de ressemblance pour chacune des distances.
La principale qualité de cet algorithme, issu d'un réseau de neurone est sa stabilité, démontrée mathématiquement [Moo 88].
Pour notre problème la stabilité des prototypes appris n'est pas un élément crucial, nous nous contenterons donc d'utiliser un algorithme de segmentation automatique simple inspiré par ART-1. Cet algorithme n'utilisera qu'une seule définition de distance et n'impose aucune contrainte dans l'évolution des prototypes. En effet il ne sera pas gênant qu'un prototype retrouve plusieurs fois la même forme au cours de l'apprentissage. Il suffit de pouvoir différencier et reconnaître des formes. L'apparence des éléments du dictionnaire et la façon dont ceux-ci évoluent n'ont aucune importance.
Voici l'algorithme que nous utiliserons :
- Rechercher dans le dictionnaire la forme q la plus proche de f :
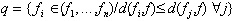(Si plusieurs
prototypes vérifient ce critère, en choisir un, au hasard, ou selon un deuxième
critère de ressemblance, i.e. refaire le même traitement sur cet ensemble
trouvé à l'aide d'une autre distance entre matrices.) - Si q == vide ou d(q,f) > Seuil(*) alors
Dictionnaire :=
Dictionnaire + f
Sinon mise à jour du prototype q : q := aq+(1-a)f avec a E [0;1] - retourner q (le n° de prototype) et le nouveau dictionnaire
Notre opérateur de mise à jour d'un élément du dictionnaire est une moyenne pondérée des matrices (moyenne des composantes une à une) dont le paramètre a permet de répartir l'importance de l'acquis face à la nouveauté :
- a = 1, les prototypes n'évoluent pas.
- a = 0, le prototype est remplacé par la forme à reconnaître.
Pour la suite nous avons utilisé a= 0.5
(*) Le seuil détermine la "finesse" du dictionnaire : plus il est bas, plus on insérera de prototypes dans le dictionnaire. Par contre, s'il est élevé, une forme considérée comme différente du prototype précédemment ne le sera plus ; on tolère donc ici plus de dissimilitudes entre un objet et son prototype. Ce seuil sera à ajuster avec soin pour avoir un dictionnaire reflétant bien l'ensemble des objets appris. S'il est trop bas, le bruit de l'image, les erreurs d'échantillonnage (dues à la numérisation de l'image) et de normalisation, impliqueront la création d'un nouveau prototype pour un objet déjà rencontré, mais, s'il est trop haut, on risque de confondre deux objets différents.
L'exemple exposé ici n'a pour objet que d'illustrer le fonctionnement de l'algorithme. L'image analysée est une image capturée à l'aide du logiciel Visilog. Elle est composée de 256x256 pixels en 256 niveaux de gris. Elle représente une scène composée de divers petits objets ; dés, pièces de monnaie, stylo... Les prototypes sont des matrices 24x24 pixels en 256 niveaux de gris également. Enfin le dictionnaire était vide avant le traitement.
Image Source : Image Visilog 256x256 pixels en 256 niveaux de gris
Cette image sera filtrée puis binarisée pour que l'extraction des formes puissent avoir lieu. L'extraction consiste à isoler chaque tache connexe de l'image binarisée, une telle tache correspondant à un objet sur l'image originelle.
Détéction des différentes formes connexes présentes dans l'image
Toutes ces formes sont ensuite normalisées : orientées et réduites dans une matrice de 24 pixels de cotés pour ensuite être comparées aux éléments du dictionnaire
Formes extraites puis normalisées
Le dictionnaire est mis à jour en examinant une à une les formes normalisées obtenues. Chaque objet est comparé aux objets appris. Le prototype le plus ressemblant est modifié (voir le prototype 1 qui correspond aux pièces de monnaies et comporte une ébauche de trou dû au rouleau de papier adhésif représenté en jaune ci-dessus). S'il n'existe pas dans le dictionnaire d'objets suffisamment ressemblant, on lui ajoute ce nouvel élément.
Dictionnaire de prototypes appris
On obtient comme description de l'image, une liste des objets qui la composent :
- 2 objets n°10 : stylos,
- 6 objets n°1 : 5 pièces de monnaie et un rouleau de papier adhésif,
- 1 objet n°4 : briquet...
| Résultat de l'interprétation de l'image : Liste des objets perçus, position, orientation et taille de ces objets |
||||
| N° Objet | Abscisse | Ordonnée | Orientation | Echelle |
| 1 | 25.56 | 212.52 | -103.79° | 1.24 |
| 2 | 118.14 | 210.09 | 72.38° | 2.33 |
| 1 | 170.87 | 191.87 | 72.52° | 1.15 |
| 3 | 61.98 | 203.45 | -96.58° | 2.89 |
| 4 | 216.35 | 192.18 | -84.39° | 2.94 |
| 5 | 148.16 | 144.33 | 17.74° | 1.76 |
| 1 | 106.79 | 136.55 | -109.48° | 1.19 |
| 6 | 72.48 | 133.34 | -68.25° | 1.01 |
| 6 | 194.30 | 105.51 | 72.14° | 1.00 |
| 7 | 134.79 | 99.91 | -113.72° | 0.99 |
| 1 | 94.77 | 85.83 | -107.82 | 1.29 |
| 8 | 230.25 | 93.34 | -67.33° | 1.95 |
| 1 | 33.09 | 77.27 | 97.57° | 1.31 |
| 9 | 167.75 | 69.80 | -95.65° | 2.31 |
| 10 | 64.21 | 87.07 | 118.31° | 5.98 |
| 11 | 29.46 | 36.71 | 42.88° | 1.90 |
| 1 | 62.26 | 28.33 | -87.40° | 1.34 |
| 10 | 181.62 | 24.35 | -168.82° | 5.53 |
Pour que la perception soit efficace elle doit être rapide et les objets pouvant être manipulé par le robot sont relativement simples et petits. Nous avons modifié la résolution des images sources en 128x128 pixels et utilisé des prototypes de 16 pixels de cotés. Ainsi il a été possible d'exécuter toute la chaîne de perception décrite dans ce chapitre en une dizaine de secondes (386 SX 20) contre plusieurs minutes pour l'exemple exposé précédemment (486 DX 33).
Les capacités de reconnaissance dépendent des objets rencontrés. La géométrie de certaines formes créé des ambiguïtés d'orientation et le système insère dans le dictionnaire plusieurs prototypes différents dans son dictionnaire pour un même objet. L'orientation étant fondée sur la recherche du point le plus éloigné du centre de gravité [E&T 95], tout objet possédant plusieurs points satisfaisant cette définition aura plusieurs orientations possibles (une pour chacun de ces points). Une recherche des axes principaux d'inertie permettrait dans la plupart des cas de lever cette ambiguïté mais la lourdeur de la méthode augmenterait considérablement les temps de calcul [C&S 95].
| Ambiguïté d'orientation | ||
| Forme perçue | Orientation 1 | Orientation 2 |
 |
 |
 |
Une autre source de multiplication des prototypes provient de la prise de vue elle même : la scène est vue de dessus pour en obtenir une image en deux dimensions. Selon leur épaisseur, l'image des objets est plus ou moins déformé par la perspective : un cube au centre de l'image sera perçu comme un carré alors qu'un même cube en bordure d'image sera perçu comme un hexagone irrégulier.
| Déformation par la perspective | |
| Objet visualisé | Forme perçue |
 |
 |
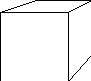